00:06 Today we meet up with Károly, who wrote a book called Optimizing
Collections.
00:54 He'll help us optimize our SortedArray type, which we wrote in
episode
#35. This
simplified version is constrained to work with Comparable elements:
import Foundation
struct SortedArray<Element: Comparable> {
var elements: [Element]
init<S: Sequence>(unsorted: S) where S.Iterator.Element == Element {
elements = unsorted.sorted()
}
mutating func insert(_ element: Element) {
elements.append(element)
elements.sort()
}
}
Optimizing insert
01:24 The insert method appends the new element and sorts the entire
array again. By making the method a little bit more complex, we can improve the
execution time.
01:52 We know the elements array is already sorted, so there's no
reason to sort the entire array after inserting one new element. Instead, we can
find the correct position at which to insert the new element.
02:28 One way of finding the correct position is by implementing binary
search, which works by iterating over a range beginning with the entire array
and splitting the range in half until it's narrowed down to one position in the
array.
03:01 We define the range's initial bounds:
mutating func insert2(_ element: Element) {
var start = elements.startIndex
var end = elements.endIndex
while start < end {
}
}
03:45 In the while loop, we could find the middle index by calculating
it, like so:
let middle = (start + end) / 2
04:01 The problem is that the addition might overflow if the array is
huge, thereby crashing the application. We avoid this by adding half the
distance to the start index:
let middle = start + (end - start) / 2
05:01 Using the middle index, we can compare the middle element and the
element that's to be inserted. If the middle element is less than the new
element, we know that all elements of the first half of the array are less than
the new element. In such a case, we can eliminate the first half and look at the
second half. We update the start index accordingly:
if elements[middle] < element {
start = middle + 1
}
05:48 Because we checked that the middle element is less than the new
element, we can update start to be the index after the middle index.
06:19 Otherwise, if the element is less than or equal to the middle
element, we have to continue with the left half. In that case, we update the
end index:
if elements[middle] < element {
start = middle + 1
} else {
end = middle
}
06:58 After the while loop, the start and end indices should be
equal. We add an assertion for this:
assert(start == end)
07:33 We've found the position at which to insert the new element. This
completes the method:
mutating func insert2(_ element: Element) {
var start = elements.startIndex
var end = elements.endIndex
while start < end {
let middle = start + (end - start) / 2
if elements[middle] < element {
start = middle + 1
} else {
end = middle
}
}
assert(start == end)
elements.insert(element, at: start)
}
07:54 Now we check our new insertion method:
var test = SortedArray<Int>(unsorted: [])
test.insert2(5)
test.insert2(4)
test.insert2(6)
Benchmarking
08:43 To test if the new implementation is faster, we can use a
benchmarking application Károly wrote, called
Attabench.
09:32 We prepared an empty benchmark, to which we'll add some tasks to
measure:
import Foundation
import BenchmarkingTools
func randomArrayGenerator(_ size: Int) -> [Int] {
var values: [Int] = Array(0 ..< size)
values.shuffle()
return values
}
public func generateBenchmarks() -> [BenchmarkProtocol] {
return []
}
func sampleBenchmark() -> BenchmarkProtocol {
let benchmark = Benchmark(title: "Insertion", inputGenerator: randomArrayGenerator)
return benchmark
}
func containsBenchmark() -> BenchmarkProtocol {
let benchmark = Benchmark(title: "Contains", inputGenerator: randomArrayGenerator)
return benchmark
}
10:03 We can add a task with a title and a closure containing code to be
measured. The closure will receive an array of random integers. We add tasks for
insert and insert2 in order to compare the two implementations. In both
cases, we start out with an empty SortedArray and loop through the random
input array to insert each value:
func sampleBenchmark() -> BenchmarkProtocol {
let benchmark = Benchmark(title: "Insertion", inputGenerator: randomArrayGenerator)
benchmark.addSimpleTask(title: "SortedArray.insert") { input in
var array = SortedArray<Int>(unsorted: [])
for value in input {
array.insert(value)
}
}
benchmark.addSimpleTask(title: "SortedArray.insert2") { input in
var array = SortedArray<Int>(unsorted: [])
for value in input {
array.insert2(value)
}
}
return benchmark
}
12:14 In order for the application to find this benchmark, we have to
add it to the return value of generateBenchmarks():
public func generateBenchmarks() -> [BenchmarkProtocol] {
return [
sampleBenchmark()
]
}
12:32 When we run this, the macOS application launches and we can find
the benchmark tasks in its menu. After starting the execution, a graph is
plotted showing measurements of the executed tasks, and we see a big difference
between the two insertion methods. The slower insert task's graph looks like a
parabola, but it's hard to see the shape of insert2, which almost appears as
constant time:
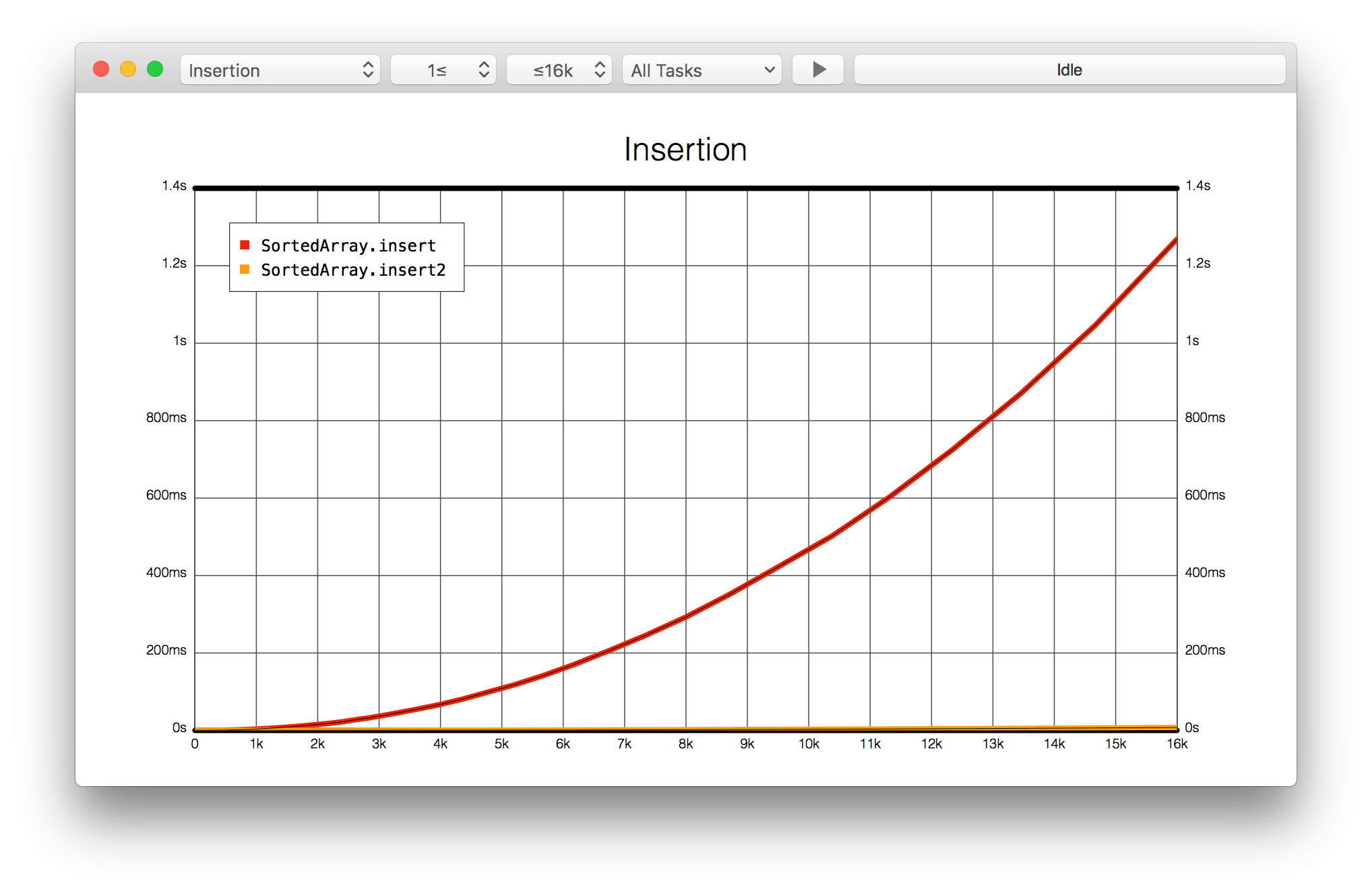
13:40 By switching the vertical time axis to a logarithmic scale, we see
that the two tasks have a similar shape. But now we notice we have the same
problem on the horizontal axis — it's hard to tell what's happening at the lower
values on the left:
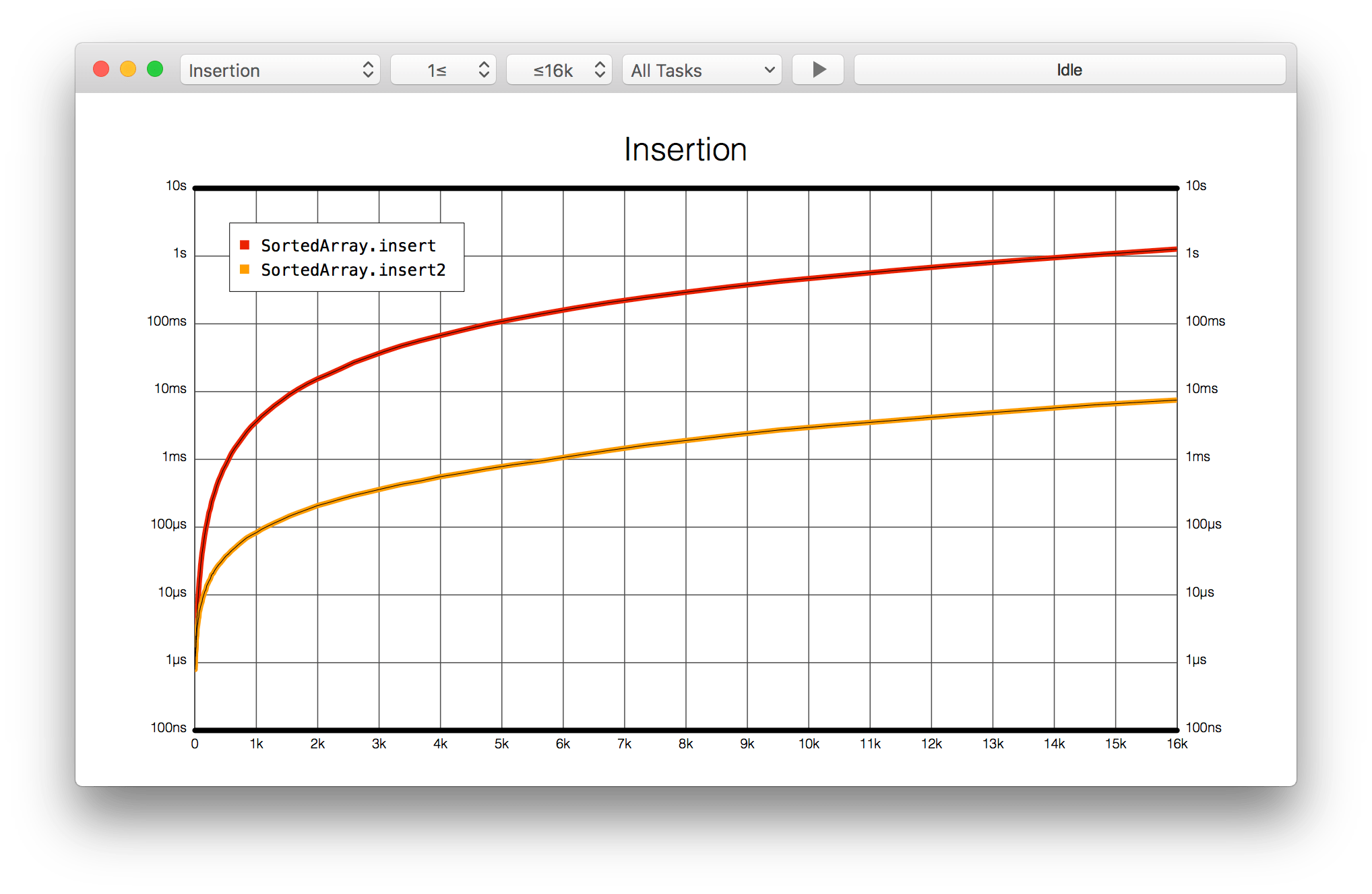
14:41 The ideal chart for benchmarks has both axes on a logarithmic
scale, so we can properly see how the tasks compare and perhaps detect patterns
that aren't normally visible. Because a logarithmic plot allocates the same
amount of space to each order of magnitude, it's easy to see at a glance how an
algorithm behaves across the board:
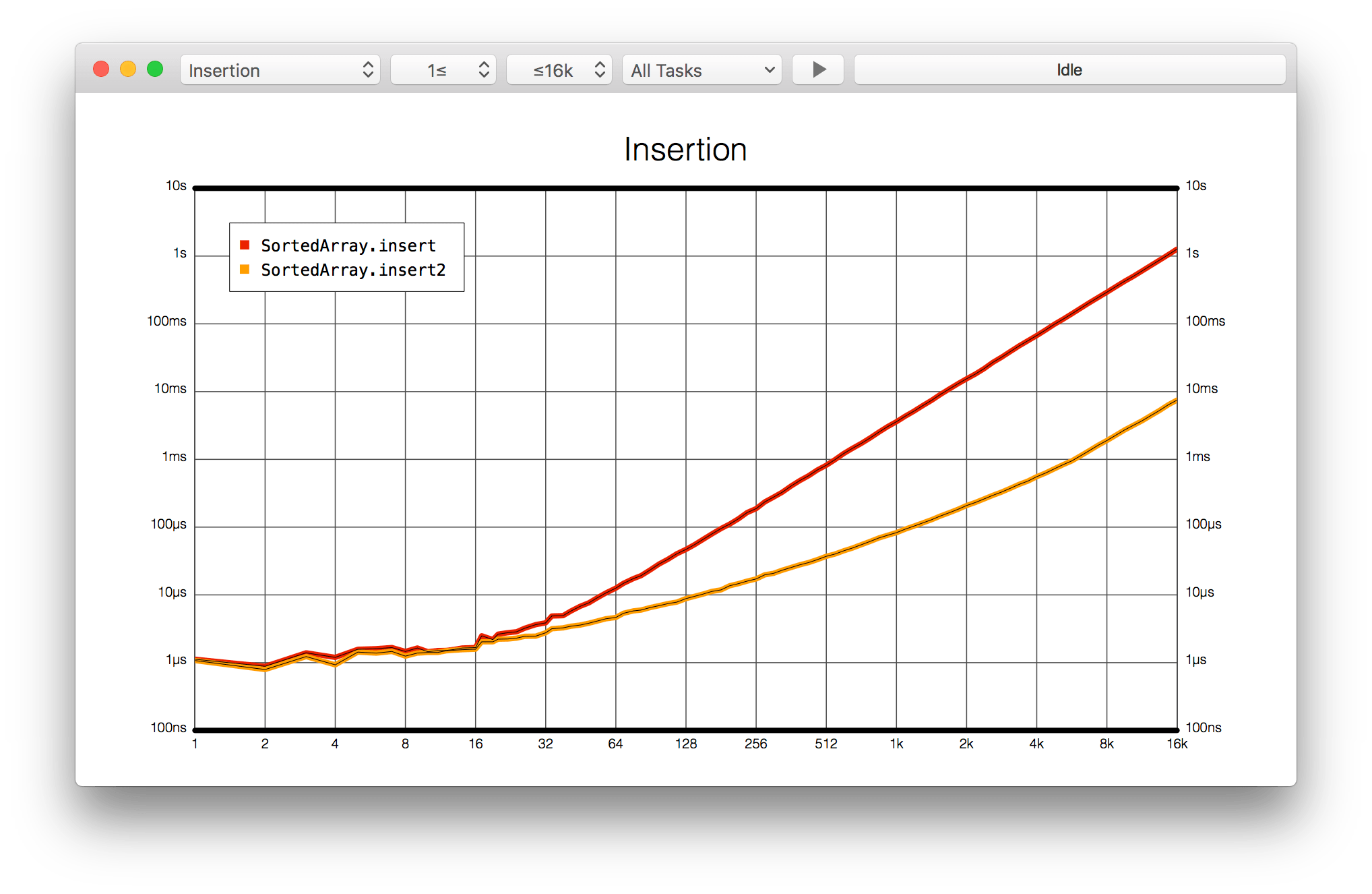
15:17 Currently, the graph shows the overall execution time for our
benchmarks, but we're more interested in the average time it takes to do a
single insertion. Fortunately, the benchmark tool offers a way to divide the
execution time by the size of the array. This gives us an amortized chart, which
displays the average time for a single insertion, plotted against array size:
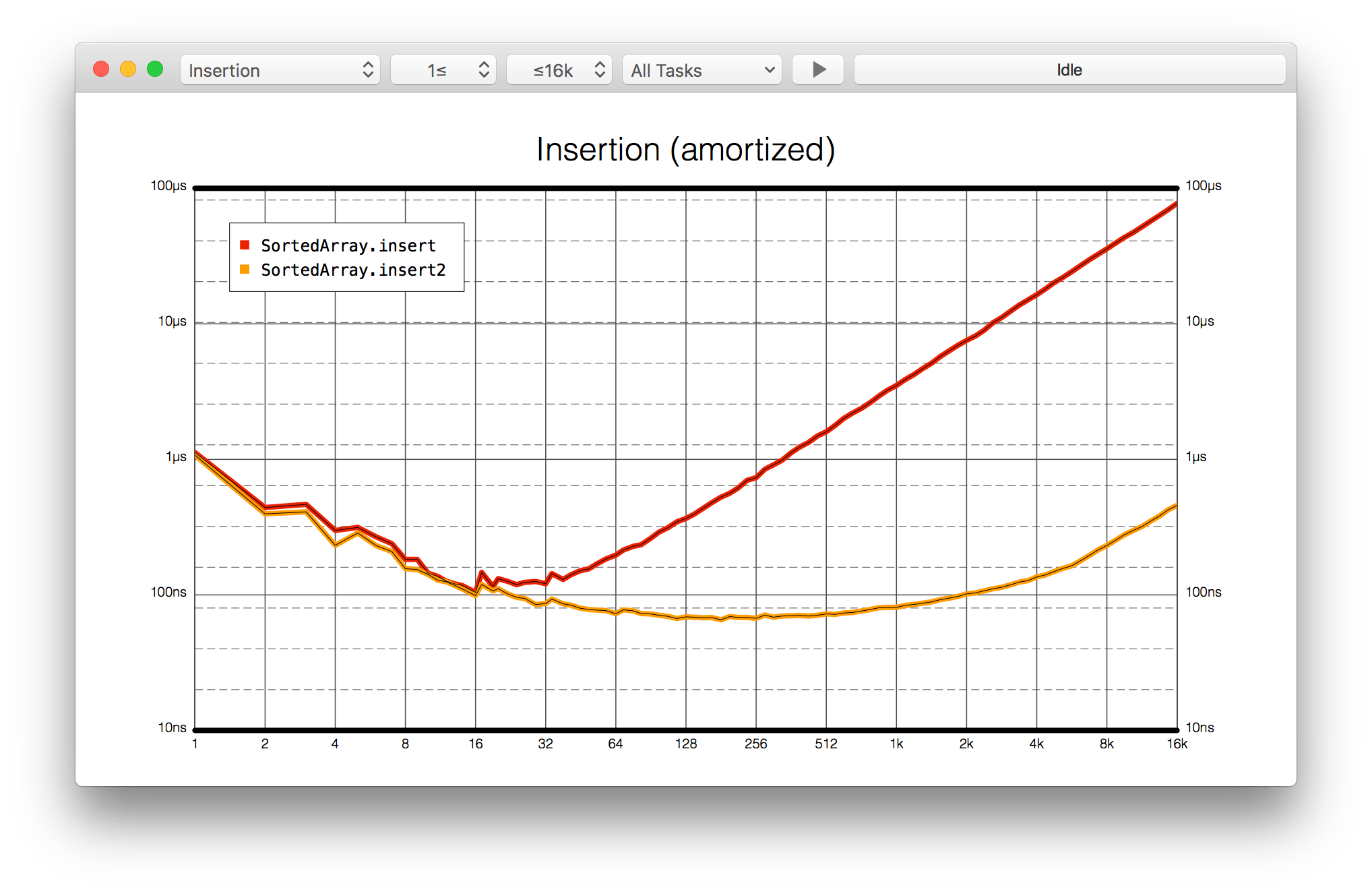
16:08 Now the graph gets interesting. When we continue the benchmark, we
can tell that our new implementation of insert2 is about 200 times faster than
the original insert. That's quite impressive for a small modification of our
code.
Optimizing contains
17:11 We can also try to make contains faster. We move some of the
code into a utility method we can reuse:
struct SortedArray<Element: Comparable> {
func index(for element: Element) -> Int {
var start = elements.startIndex
var end = elements.endIndex
while start < end {
let middle = start + (end - start) / 2
if elements[middle] < element {
start = middle + 1
} else {
end = middle
}
}
assert(start == end)
return start
}
mutating func insert2(_ element: Element) {
elements.insert(element, at: index(for: element))
}
}
18:48 To write contains2, we can use index(for:) to check whether
the element already exists at the index where it belongs. We should check that
the returned index is not the array's endIndex. Otherwise, we'd get an
out-of-bounds exception by using subscript:
func contains2(element: Element) -> Bool {
let index = self.index(for: element)
guard index < elements.endIndex else { return false }
return self[index] == element
}
19:56 We can benchmark this method too — except this time, we have to
start with a populated array before we can measure the execution of the
contains method. To add the task, we use a different method in which we have
to return a closure that takes a timer and uses it to measure a specific block
of code. This way, we can put the setup of the SortedArray outside the
measured code:
func containsBenchmark() -> BenchmarkProtocol {
let benchmark = Benchmark(title: "Contains", inputGenerator: randomArrayGenerator)
benchmark.addTask(title: "Sequence.contains") { input in
let array = SortedArray<Int>(unsorted: input)
return { timer in
timer.measure {
for value in input {
if !array.contains(value) { fatalError() }
}
}
}
}
benchmark.addTask(title: "SortedArray.contains2") { input in
let array = SortedArray<Int>(unsorted: input)
return { timer in
timer.measure {
for value in input {
if !array.contains2(element: value) { fatalError() }
}
}
}
}
return benchmark
}
24:08 We add the new benchmark to the list of available benchmarks:
public func generateBenchmarks() -> [BenchmarkProtocol] {
return [
sampleBenchmark(),
containsBenchmark()
]
}
24:19 We run the application and choose the "Contains" benchmark. Then
we see the amortized chart:
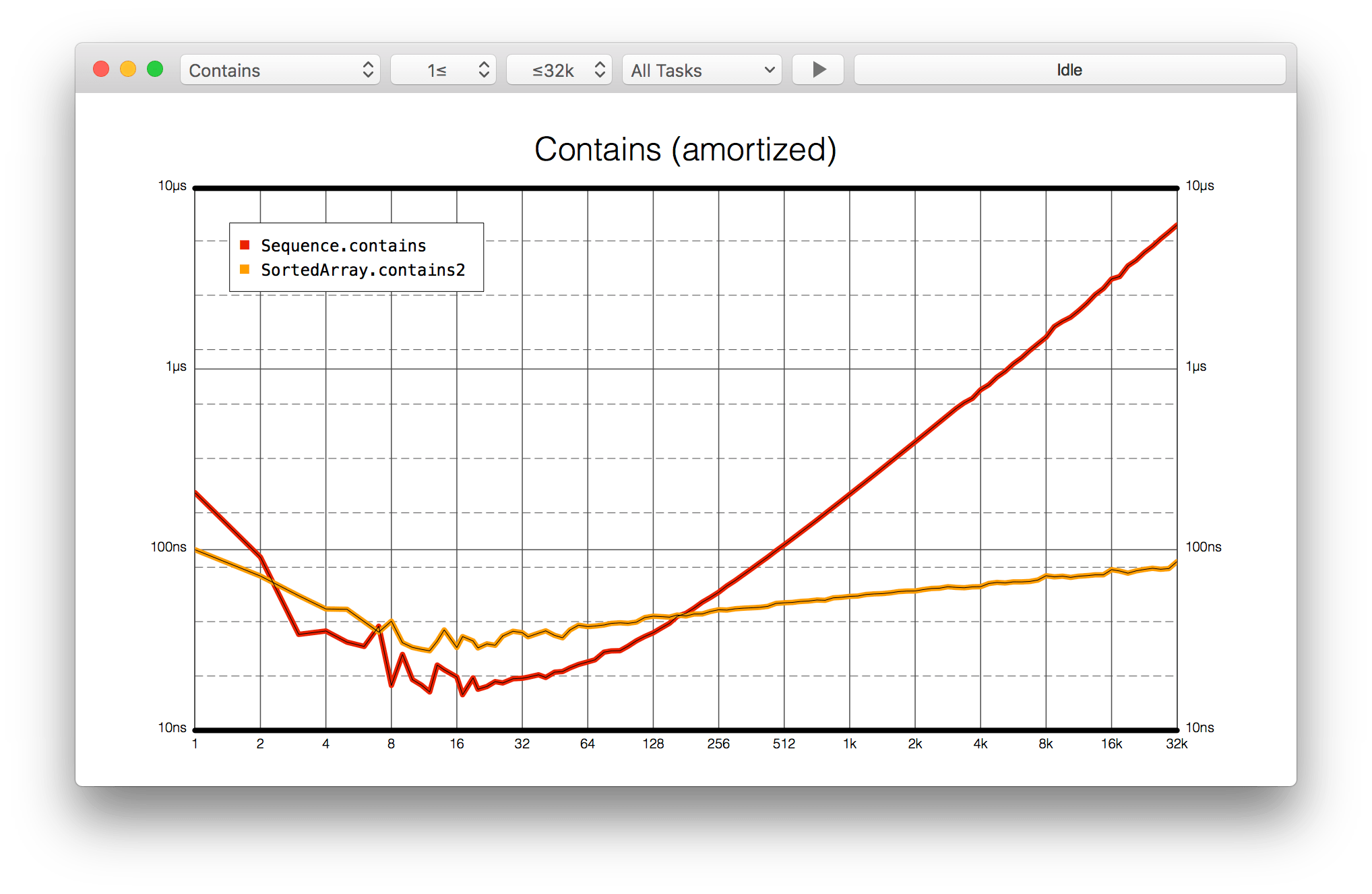
24:39 It appears that the original implementation of contains — which
enumerates and compares each element — is faster for small arrays than our new
version is. That's probably because the CPU can prefetch values when iterating
over a continuous buffer. Besides, the algorithm of contains itself is much
simpler, whereas the more complicated contains2 adds some overhead by doing
comparisons. However, the time difference is very small: in the worst case, with
an array of around 16 elements, the difference in execution time of the two
methods is a couple dozen nanoseconds.
26:37 There's a lot more to do with collection optimization. We'll
continue exploring in a future episode.